History and Archives

"Golden Books" - Observations in Particle Physics from Two Neutrinos to the Standard Model

	Observations in Particle Physics from Two Neutrinos to the Standard Model Leon M. Lederman

 

Fermi National Accelerator Laboratory
Batavia, Illinois

Operated by Universities Research Association, Inc.
Under Contract with the United States Department of Energy

 

Introduction

Leon M. Lederman, director from 1979-89 and one of the founding fathers of Fermilab, exerted a major influence on the development of the style and outreach of the Laboratory from its beginnings. One of the foremost experimental high-energy physicists in the United States, Lederman assumed the mantle of director in 1979 following an active career of particle discovery at Columbia University's Nevis Laboratory, Brookhaven National Laboratory, Lawrence Berkeley Laboratory, Cornell University's Electron Storage Rings, CERN, and Fermilab.

Well-known for his wit and naturally comic delivery in numerous public talks, "Observations in Particle Physics from Two Neutrinos to the Standard Model," written by Lederman in 1988, is the serious lecture he delivered in Stockholm, Sweden on the occasion of the presentation of the 1988 Nobel Prize in Physics. It was first published in Reviews of Modern Physics 61, 3 July 1989. This piece of his writing reveals the serious and dedicated scientist behind Lederman's smiling eyes.

Lederman's term directing Fermilab was an engaging one. As obstacles mounted, both in physics and in his administration, they were attacked and surmounted. His active involvement in technical, physical, intellectual, political, cultural, and social problems led to a well-prepared laboratory confronting the challenges of the times. Enrichment and enlightenment over a broad spectrum describe the thrust of Fermilab under his visionary guidance.

A poet at heart, Lederman has been at the front of the improvement of science education issues since the 1960s. Eloquently testifying before Congress and the American public at every opportunity, he has brought the matter to the attention of the nation, becoming spokesman for many educators, students and observers of our global condition. It is Lederman's deeply-felt concern for the future of the United States, as well as for his science, which compels him confidently onward to the front lines.

Observations in Particle Physics from Two Neutrinos to the Standard Model

I. Introduction

My colleagues Melvin Schwartz and Jack Steinberger and I, sharing the 1988 Nobel Award, were faced with a dilemma. We could, in Rashomon-like fashion, each describe the two-neutrino experiment (as it became known) in his own style, with his own recollections, in the totally objective manner of true scientists. Whereas this could be of some interest to sociologists and anthropologists, this definitely would run the risk of inducing boredom, and so we decided on a logical division of effort. Dr. Schwartz, having left the field of physics a decade ago, would concentrate on the origins and on the details of the original experiment. Dr. Steinberger would concentrate on the exploitation of neutrino beams, a field in which he has been an outstanding leader for many years. I volunteered to discuss "the rest," a hasty decision which eventually crystallized into a core theme-how the two-neutrino discovery was a crucial early step in assembling the current world view of particle physics which we call the "Standard Model." Obviously, even a "first step" rests on a preexisting body of knowledge that could also be addressed. My selection of topics will not only be subjective, but it will also be obsessively personal as befits the awesome occasion of this award ceremony.

I will relate a sequence of experiments which eventually, perhaps even tortuously, contributed to the Standard Model, that elegant but still incomplete summary of all subnuclear knowledge. This model describes the 12 basic fermion particles, six quarks and six leptons, arranged in three generations and subject to the forces of nature carried by 12 gauge bosons. My own experimental work brought me to such accelerators as the Nevis Synchrocyclotron (SC); the Cosmotron and Alternate Gradient Synchrotron (AGS) at the Brookhaven National Laboratory (BNL); the Berkeley Bevatron and the Princeton-Penn Synchrotron; the Synchrocyclotron, Proton Synchrotron (PS), and Intersecting Storage Ring (ISR) machines at CERN; the Fermilab 400-GeV accelerator; and the electron-positron collider Cornell Electron Storage Rings (CESR) at Cornell. I can only hint at the tremendous creativity which brought these magnificent scientific tools into being.

One must also have some direct experience with the parallel development of instrumentation. This equally bright record made available to me and my colleagues a remarkable evolution of the ability to record particular subnuclear events with ever finer spatial detail and even finer definition in time. My own experience began with Wilson cloud chambers, paused at photographic nuclear emulsions, exploited the advances of the diffusion cloud chamber, graduated to small arrays of scintillation counters, then spark chambers, lead-glass high-resolution Cerenkov counters, scintillation hodoscopes, and eventually the increasingly complex arrays of multiwire proportional chambers, calorimeters, ring imaging counters, and scintillators all operating into electronic data acquisition systems of exquisite complexity.

Experimentalists are often specialists in reactions initiated by particular particles. I have heard it said that there are some physicists, well along in years, who only observe electron collisions. In reviewing my own bibliography, I can recognize distinct periods, not too different from artists' phases, e.g., Picasso's Blue Period. My earliest work was with pions, which exploded into the world of physics (in 1947) at about the time I made my quiet entry. Later I turned to muons mostly to study their properties and to address questions of their curious similarity to electrons, e.g., in order to answer Richard Feynman's question, "Why does the muon weigh?" or Rabi's parallel reaction, "Who ordered that?" Muons, in the intense beams from the AGS, turned out to be a powerful probe of subnuclear happenings not only in rather classical scattering experiments (one muon in, one muon out), but also in a decidedly nonclassical technique (no muons in, two muons out). A brief sojourn with neutral kaons preceded the neutrino program, which my colleagues will have discussed in detail. This led finally to studies of collisions with protons of the highest energy possible, in which leptons are produced. This last phase began in 1968 and was still going on in the 1980s.

Accelerators and detection instruments are essentials in particle research but there also needs to be some kind of guiding philosophy. My own approach was formed by a specific experience as a graduate student.

My thesis research at Columbia University involved the construction of a Wilson cloud chamber designed to be used with the brand new 400-MeV synchrocyclotron under construction at the Nevis Laboratory about 20 miles north of the Columbia campus in New York City.

I. I. Rabi was the physics department Chairman, maestro, teacher of us all. He was intensely interested in the new physics that the highest-energy accelerator in the world was producing. At one point I described some curious events observed in the chamber which excited Rabi very much. Realizing that the data were very unconvincing, I tried to explain that we were a long way from a definitive measurement. Rabi's comment, "First comes the observation, then comes the measurement," served to clarify for me the fairly sharp distinction between "observation" and "measurement." Both experimental approaches are necessary to progress in physics. Observations are experiments which open new fields. Measurements are subsequently needed to advance these. Observations may be qualitative and may require an apparatus that sacrifices detail. Measurement is more usually concerned with the full panoply of relevant instruments. And of course, there are blurred boundaries. In the course of the next 30 or so years I have been concerned with measurements of great precision, e.g., the magnetic moment of the muon (Coffin et al., 1957), or the mass, charge, and lifetime of the muon (Devons et al., 1960), measurements of moderate precision like the rho value in muon decay, the elastic scattering of muons (Ellsworth et al., 1968), or the lifetimes of the lambda and kaon particles (Blumenfeld, Chinowsky, and Lederman, 1958). I have also been involved in observations, which are attempts to see entirely new phenomena. These "observations" have, since 1956, been so labeled in the titles of papers, some of which are listed in chronological order in Table I and as references (Laude et al., 1956; Garwin et al., 1957; Danby et al., 1962; Christenson et al., 1970; Büsser et al., 1973; Herb et al., 1977; Finocchiaro et al., 1980). I selected these because (I) I loved each one and (2) they were reasonably important in the evolution of particle physics in the amazing period from the 1950s to the 1980s.

TABLE I. Major Observations.

---

Observation of long-lived neutral V particles (Laude et al., 1956)

Observation of the failure of conservation of parity and charge conjugation in meson decays: the magnetic moment of the free muon (Garwin, Lederman, and Weinrich, 1957)

Observation of the high-energy neutrino reactions and the existence of two kinds of neutrinos (Danby et al., 1962)

Observation of massive muon pairs in hadron collisions (Christenson et al., 1970)

Observation of π mesons with large transverse momentum in high-energy proton-proton collisions (Büsser et al., 1973)

Observation of a dimuon resonance at 9.5 GeV in 400-GeV proton-nucleus collisions (Herb et al., 1977)

Observation of the upsilon 4-prime at CESR (Finocchiaro et al., 1980)

---

II. Long-Lived Neutral Kaons: Observation of a Long-Lived Neutral V Particle (Laude et al., 1956)

In 1955, Pais and Gell-Mann (cell-Mann and Pais, 1955) noted that the neutral K meson presented a unique situation in particle physics. In contrast to, e.g., the π⁰, the K⁰ is not identical to its antiparticle, even though they cannot be distinguished by their decay. Using charge-conjugation invariance, the bizarre particle mixture scheme emerges: K⁰ and K⁰ are appropriate descriptions of particle states produced with the well-defined quantum number, strangeness, but two other states, K_L and K_S, have well-defined decay properties and lifetimes.

The essence of the theoretical point, given in a Columbia University lecture by Abraham Pais in the spring of 1955, was that there should exist, in equal abundance with the already observed K_S (lifetime 10^-10 sec), a particle with much longer lifetime, forbidden by C invariance from decaying, as did K_S, into two pions. The clarity of the lecture stimulated what appeared to me to be an equally clear experimental approach, using the cloud chamber which had been invented back in 1896 by the Scottish physicist C. T. R. Wilson. The cloud chamber was first used for making visible the tracks of subatomic particles from nuclear disintegrations in 1911. Supplemented with strong magnetic fields or filled with lead plates, it became the workhorse of cosmic-ray and early accelerator research, and was used in many discoveries, e.g., those of the positron, the muon, the lambda, the "θ" (now K_S), and the K⁺. As an instrument, it was more biological than physical, subject to poisons, track distortions, and an interminable period of about one minute. To obtain precise momentum and angle measurements with cloud chambers required luck, old world craftsmanship, and a large, not-to-be questioned burden of folklore and recipes. Their slow repetition rate was a particular handicap in accelerator science. Donald Glaser's invention of the bubble chamber and Luis Alvarez's rapid exploitation of it offered a superior instrument for most purposes, and by the mid-1950s, very few cloud chambers were still operating at accelerators. At Columbia I had some success with the 11-inch-diameter chamber built at the Nevis Synchrocyclotron for my thesis, a comparison of the lifetimes of negative and positive pions (Lederman, Booth, et al., 1951). In a stirring finale to this thesis, I had concluded (wrongly as it turned out) that the equality of lifetimes implied that charge conjugation was invariant in weak interactions.

FIG. 1. Experimental arrangements for lifetime study.

In its history at Nevis, the cloud chamber produced results on the decay of pions (Lederman, Tinlot, and Booth, 1951), on the mass of the neutrino born in pion decay (Lederman, 1951) (enter the muon neutrino; it would be almost a decade before this number was improved), on the scattering of pions (Byfield et al., 1952) including the first suggestions of strong backward scattering that was later found by E. Fermi to be the indicator of the "3,3" resonance, and the Coulomb-nuclear interference of π⁺ and π^- scattering in carbon. The carbon scattering led to analysis in terms of complex opticalmodel parameters which now, over 30 years later, are still a dominating subject in medium-energy physics convocations.

FIG. 2. Example of K°→π++π- + neutral particle. P+ is shown to be a pion by ionization measurements. PA is a proton track used in the ionization calibration.

When the Cosmotron began operating in BNL about 1953, we had built a 36-inch-diameter chamber, equipped with a magnetic field of 10,000 G, to study the new Λ⁰'s and θ⁰'s, which were copiously produced by pions of ∼1 GeV. The chamber seemed ideal to use in a search for long-lived kaons. Figure 1 shows the two arrangements that were eventually used and Fig. 2 shows a K_L event in the 36-inch cloud chamber. The Cosmotron produced ample quantities of 3-GeV protons, and access to targets was particularly convenient because of the magnetic structure of the machine. The trick was to sweep all charged particles away from the chamber and reduce the sensitivity to neutrons by thinning the chamber wall and using helium as chamber gas. By mid-1956, our group of five had established the existence of K_L and had observed its principal three-body decay modes. Our discussion of alternative interpretations of the "V" events seen in the chamber was exhaustive and definitive. In the next year we measured the lifetime by changing the flight time from target to chamber (both the cloud chamber and the accelerator were immovable). This lifetime, so crudely measured, agrees well with the 1988 handbook value. The K_L was the last discovery made by the now venerable Wilson cloud chamber.

In 1958, we made a careful search of the data for the possibility of a two-body decay mode of K_L. This search was a reflection of the rapid pace of events in the period 1956-1958. Whereas C invariance was the key argument used by Pais and Gell-Mann to generate the neutral-K mixture scheme, the events of 1957 (see below) proved that, in fact, C invariance was strongly violated in weak decays. Since the predictions turned out to be correct, the improved argument, supplied by Lee, Oehme, and Yang (1957), replaced C invariance by CP invariance, and in fact, also CPT invariance. CP invariance would strictly forbid the decay

K_L→π⁺+π^-,

and, in our 1958 paper based upon 186 K_L events, we concluded ". . . only two events had zero total transverse momentum within errors . . . and none of these could be a two-body decay of the K⁰_L. An upper limit to K⁰_L→π⁺+π^- was set at 0.6% ... the absence of the two-pion final state is consistent with the predictions of time reversal invariance" (Bardon et al., 1958).

Six years later, at the much more powerful AGS accelerator, V. Fitch and J. Cronin (Christenson et al., 1964), capitalizing on progress in spark-chamber detectors, were able to vastly increase the number of observed K_L decays. They found clear evidence for the two-pion decay mode at the level of 0.22%, establishing the fact that CP is, after all, not an absolute symmetry of nature.

The K⁰ research eventually provided a major constraint on the Standard Model. On the one hand, it served to refine the properties of the strange quark proposed in 1963 by Gell-Mann. On the other hand, the famous Kobayashi-Maskawa (KM) quark mixing matrix, with three generations of quarks, was an economical proposal to accommodate the data generated by the K⁰ structure and the observation of CP violation. Finally the neutral-K-meson problem (essentially the K_S decay modes) led to the next major observation, that of charge conjugation (C) and parity (P) violation and, together, a major advance in the understanding of the weak interactions. In 1988, neutral-K research remains a leading component of the fixed-target measurements at Fermilab, BNL, and CERN.

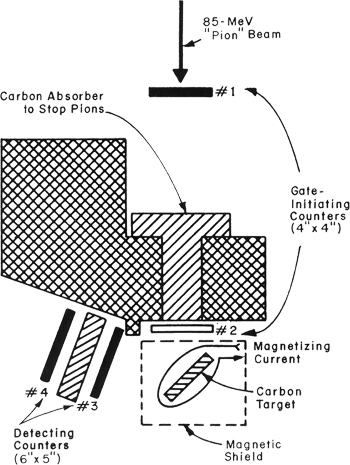
III. Observation of the Failure of Conservation of Parity and Charge Conjugation in Meson Decays (Garwin et al., 1957)

In the summer of 1956 at BNL, Lee and Yang had discussed the puzzle of the K's (θ,τ puzzle) and were led to propose a number of reactions where possible P violation could be tested in weak interactions (Lee and Yang, 1956). At first glance these all seemed quite difficult experimentally, since one was thinking of relatively small effects. Only C.S. Wu, our Columbia colleague, attempted, with her collaborators at the National Bureau of Standards, the difficult problem of polarizing a radioactive source. When, at a Christmas party in 1956, Wu reported that early results indicated large parity-violating effects in the decay of Coh0, it became conceivable that the chain of parity-violating reactions: π→μ+ν and then μ→e+2ν would not reduce the parity-violating effect to unobservability. The "effect" here was the asymmetry in the emission of electrons around the incident, stopped, and spinning polarized muon.

Experience in two key areas set in motion a series of events which would convert a Friday Chinese-lunch discussion, just after New Year's, 1957, into a Tuesday morning major experimental observation. One was that I knew a lot about the way pion and muon beams were formed at the Nevis cyclotron. In 1950, John Tinlot and I had been pondering how to get pions into the cloud chamber. Until that time, external beams of pions were unknown at the existing cyclotrons such as those at Berkeley, Rochester, and Liverpool. We plotted the trajectories of pions produced by 400-MeV protons hitting a target inside the machine, near the outer limit of orbiting protons, and we discovered fringe-field focusing. Negative pions would actually emerge from the accelerator into a well collimated beam. It remained only to invent a target holder and to modify the thick concrete shield so as to "let them out." In about a month, we had achieved the first external pion beam and had seen more pions in the cloud chamber than had ever been seen anywhere.

The second key area had to do with my student, Marcel Weinrich, who had been studying the lifetime of negative muons in various materials. To prepare his beam we had reviewed the process of pions converting to muons by decay-in-flight. What was more subtle but easy to play back during the 30-minute Friday evening drive from Columbia to Nevis was that a correlation of the muon spin relative to its CM momentum would, in fact, be preserved in the kinematics of pion decay-in-flight, resulting in a polarized muon beam. One totally unclear issue was whether the muon would retain its polarization as it slowed from -50 MeV to rest in a solid material. Opportunities to pick up an electron and depolarize seemed very large, but I recalled Rabi's dictum: "A spin is a slippery thing" and decided - why not try it?

 

FIG. 4. Variation of gated 3-4 minting rate with magnetizing current. The solid curve is computed from an assumed electron angular distribution I-1/3 cosθ, with counter and gate-width resolution folded in.

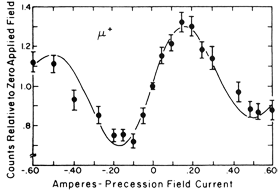
Preempting Weinrich's apparatus and enlisting Richard Garwin, an expert on spin precession experiments (as well as on almost everything else), we began the Friday night activities which culminated, Tuesday morning, in a 50-standard-deviation parity-violating asymmetry in the distribution of decay electrons relative to muon spin. Figure 3 shows the very simple arrangement and Fig. 4 shows the data. The following 10 conclusions were contained in the publication of our results.

Not bad for a long weekend of work.

This large effect established the two-component neutrinos and this, together with details of the decay parameters as they emerged over the next year, established the V -A structure of the weak interactions. A major crisis emerged from the application of this theory to high energy, where the weak cross section threatened to violate unitarity. Theoretical attempts to prevent this catastrophe ran into the absence of evidence for the reaction

μ→e+γ .

The rate calculated by Columbia colleague G. Feinberg (1958) was 104 times larger than that of the data. This crisis, as perceived by Feinberg, by T. D. Lee, and by Bruno Pontecorvo, provided motivation for the two-neutrino experiment. The stage was also set for increasingly sharp considerations of the intermediate vector-boson hypothesis and, indeed, ultimately the electroweak unification.

The 1957 discovery of parity violation in pion and muon decay proved to be a powerful tool for additional research and, indeed, it kept the "pion factories" at Columbia, Chicago, Liverpool, CERN, and Dubna going for decades, largely pursuing the physics that polarized muons enabled one to do. The earliest application was the precise magnetic resonance measurement of the muon magnetic moment at Nevis in 1957 (Coffin et al., 1957). The high level of precision in such measurements had been unknown to particle physicists, who had to learn about precisely measured magnetic fields and spin flipping. A more profound followup on this early measurement was the multidecade obsession at CERN with the g value of the muon. This measurement provides one of the most exacting tests of quantum electrodynamics and is a very strong constraint on the existence of hypothetical particles whose coupling to muons would spoil the current excellent agreement between theory and experiment.

One conclusion of the 1957 parity paper states hopefully that, ". . . it seems possible that polarized positive and negative muons will become a powerful tool for exploring magnetic fields in nuclei, atoms, and interatomic regions." Today "μSR" (muon spin resonance) has become a widespread tool in solid-state and chemical physics, meriting annual conferences devoted to this technique.

IV. Observation of High-Energy Neutrino Reactions and the Existence of Two Kinds of Neutrinos (Danby et al., 1962)

Since this is the subject of Melvin Schwartz's paper I will not review the details of this research.

The two-neutrino road (a better metaphor would perhaps be a piece of the jigsaw puzzle) to the Standard Model passed through a major milestone with the 1963 quark hypothesis. In its early formulation by both Gell-Mann and George Zweig, three quarks, i.e., a triplet, were believed adequate along the lines of other attempts at constituent explanations (e.g., the Sakaka model) of the family groupings of hadrons.

Before the quark hypothesis, a feeling for baryon-lepton symmetry had motivated many theorists, one even opposing the two-neutrino hypothesis before the experiment because ". . . two types of neutrinos would imply two types of protons." However, after the quark flavor model, Bjorken and Glashow (1964) transformed the baryon-lepton symmetry idea to quarklepton symmetry and introduced the name "charm." They predicted the existence of a new family of particles carrying the charm quantum number. This development, and its enlargement by the Glashow -Iliopolis-Maiani (GIM) mechanism in 1970, was another important ingredient in establishing the Standard Model (Glashow et al., 1970).

In GIM, the quark family structure and weak-interaction universality explain the absence of strangeness-changing neutral weak decays. This is done by assuming a charmed quark counterpart to the second neutrino ν_μ With the 1974 discovery of the J/ψ at BNL/Stanford Linear Accelerator Center (SLAC) and subsequent experiments establishing the c quark, the Standard Model, at least with two generations, was experimentally established. Included in this model was the doublet structure of quarks and leptons, e.g., (u,d), (c,s), (e, ν_e), (μ,ν_μ) .

The measurements that followed from this observation are given in detail in Jack Steinberger's paper. Major neutrino facilities were established at BNL, CERN, Serpukhov, and Fermilab. Out of these came a rich yield of information on the properties of the weak interaction, including neutral as well as charged currents, on the structure functions of quarks and gluons within protons and neutrons, and on the purely leptonic neutrino-electron scattering.

V. Partons and Dynamical Quarks

A. Observation of dimuons in 30-GeV proton collisions (Christenson et al., 1970)

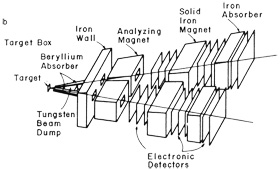
The two-neutrino experiment moved, in its followup phase at BNL, to a much more massive detector and into a far more potent neutrino beam. To provide for this, the AGS proton beam was extracted from the accelerator, not at all an easy thing to do because an extraction efficiency of only 95% would leave an unacceptably large amount of radiation in the machine.

However, the ability to take pi ons off at 0° to the beam, rather than at the 7° of the original experiment, represented a very significant gain in pions, hence in neutrinos. Thus the second neutrino experiment, now with healthy competition from CERN, could look forward to thousands of events instead of the original 50.

The major motivation was to find the W particle. The weak-interaction theory could predict the cross section for any given mass. The W production was

ν_μ+A→W⁺+μ ^- +A^*,

ν_μ+A→W^-+μ⁺+A^*.

FIG. 2. (a) Neutrino event with long muon and possible second μ meson. (b) Neutrino event with long muon and possible electron.

Since W will immediately decay, and often into a charged lepton and neutrino, two opposite-sign leptons appear in the final state at one vertex. Figures 5(a) and 5(b) show W candidates. The relatively low energy of the BNL and CERN neutrino beams produced by 30-GeV protons (E∼ I GeV) made this a relatively insensitive way of searching for W's, but both groups were able to set limits,

M_W>2 GeV.

We were then stimulated to try to find W's produced directly with 30GeV protons, the signature being a high-transverse-momentum muon emerging from W decay (∼M_W/2). The experiment found no large momentum muons and yielded (Burns et al., 1965) an improved upper limit for the W mass of about 5 GeV, which, however, was burdened by theoretical uncertainties of how W's are produced by protons. The technique led, serendipitously, to the opening of a new field of high-energy probes.

To look for W's, the neutrino-producing target was removed and the beam of protons was transported across the former flight path of 22 m (for pions) and buried in the thick neutrino shield. The massive W could show itself by the appearance of high-transverse-momentum muons. This beam dump approach was recognized in 1964 to be sensitive to short-lived neutrino sources (Okun, 1966; Yamaguchi, 1986), e.g.; heavy leptons produced by 30-GeV protons. However, the single muon produced by a hypothetical W could also have been a member of a pair produced by a virtual photon. This criticism, pointed out by Y. Yamaguchi (1966) and L. Okun (1966), presented us with the idea for a new small-distance probe: virtual photons.

We promptly began designing an experiment to look for the virtualphoton decay into muon pairs with the hope that the decreasing yield as a function of effective mass of the observed pair is a measure of small distance physics and that this slope could be interrupted by as yet undiscovered vector mesons. Observation here would be using the illumination of virtual photons whose parameters could be determined from the two-muon final state. In 1967, we organized a relatively simple exploration of the yield of muon pairs from 30-GeV proton collisions. Emilio Zavattini from CERN, Jim Christenson, a graduate of the FitchCronin experiment from Princeton, and Peter Limon, a postdoc from Wisconsin, joined the proposal. Figure 6 shows the apparatus and Fig. 7 shows the data. Later we were taught (by Richard Feynman) that this was an inclusive experiment:

p + U→μ⁺ +μ^- + anything.

FIG. 6. Brookhaven dimuon setup.

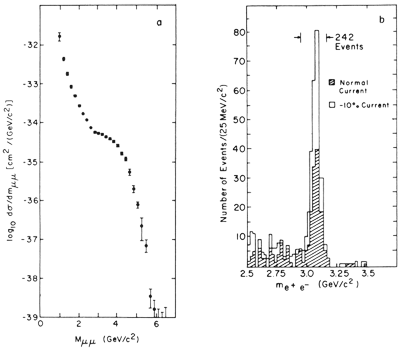
The yield of muon pairs decreased rapidly from 1 GeV to the kinematic limit of nearly 6 GeV with the exception of a curious shoulder near 3 GeV. The measurement of muons was by range as determined by liquid and plastic scintillation counters interspersed with steel shielding. Each angular bin (there were 18) had four range bins, and for two muons this made a total of only 5000 mass bins into which to sort the data. Multiple scattering in the minimum of 10 feet of steel made finer binning useless. Thus we could only note that "Indeed, in the mass region near 3.5 GeV, the observed spectrum may be reproduced by a composite of a resonance and a steeper continuum." This 1968-1969 experiment was repeated in 1974 by Aubert et al. (1974), with a magnetic spectrometer based upon multiwire proportional chambers. The shoulder was refined by the superior resolution into a towering peak [see Fig. 7(a)] called the "J" particle.

Our huge flux of 10¹¹ protons/pulse made the experiment very sensitive to small yields and, in fact, signals were recorded at the level of 10^-12 of the total cross section. A crucial development of this class of superhigh-rate experiments was a foolproof way of subtracting accidentals.

 

The second outcome of this research was its interpretation, by S. Drell and T-M. Yan. They postulated the production of virtual photons by the annihilation of a quark and antiquark in the colliding particles. The application of the now firmly named Drell-Yan process (this is how theorists get all the credit) in unraveling of quark dynamics has become increasingly incisive. It lagged behind the deeply inelastic scattering (DIS) analysis by Bjorken and others, in which electrons, muons, and neutrinos were scattered from nucleons with large energy loss. The Drell-Yan process is more dependent upon the strong-interaction processes in the initial state and is more subject to the difficult problem of higher-order corrections. However, the dilepton kinematics gives direct access to the constituent structure of hadrons with the possibility of experimental control of important parameters of the parton distribution function. Indeed, a very large Drell-Yan industry now flourishes in all the proton accelerators. DrellYan processes also allow one to study structure functions of pions, kaons, and antiprotons.

A major consequence of this experimental activity, accompanied by a much greater theoretical flood (our first results stimulated over 100 theoretical papers), was a parameter-free fit of fairly precise (timelike) data (Kaplan et al., 1978; Ito et al., 1981) of "two leptons out" to nucleon structure functions determined by probing the nuclear constituents with incident leptons. Some of the most precise data he-re were collected by the CDHS group of Jack Steinberger, and he has covered this in his paper. The agreement of such diverse experiments on the behavior of quark-gluon constituents went a long way toward giving quarks the reality of other elementary particles, despite the confinement restriction.

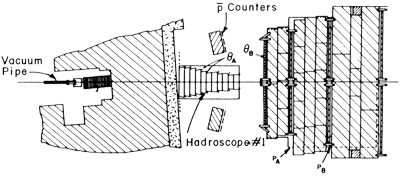
B. Observation of π mesons with large transverse momentum in highenergy proton-proton collisions (Büsser et al., 1973)

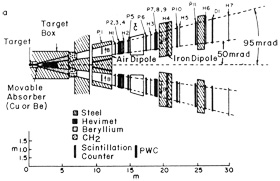
The dynamics of quark-parton constituents were first convincingly demonstrated by James Bjorken's analysis and interpretation of the DIS experiments at SLAC in 1970. Feynman's parton approach must, of course, also be mentioned. The Berman-Bjorken-Kogut (BBK) paper (1971) became the Bible of hard collisionists. In 1971, the brand new ISR at CERN began operations, and experimenters were able to observe head-on collisions of 30-GeV protons on 30-GeV protons. The ISR, as the highest-energy machine in the 1970s, was a superb place to practice observation strategy. Impressed by the power of the dilepton probe at BNL and by its hints of structure, Rodney Cool of Rockefeller University and I co-opted Luigi DiLella from CERN to help us design an approach that would trade luminosity for resolution. Recall that with the "beam dump" philosophy at BNL we had been able to observe dimuon yields as low as 10^-12 of the total cross section. However, the penalty was a resolution roughly analogous to using the bottom of a CocaCola bottle as the lens for a Nikon. The balance of resolution and luminosity would be a crucial element in the increasing power of the dilepton process.

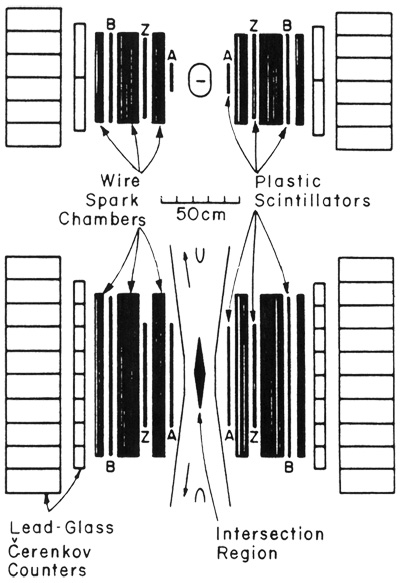
FIG. 8. CCR apparatus, CERN ISR

We learned from Carlo Rubbia about the excellent properties of lead glass as an electromagnetic spectrometer. Photons or electrons would multiply in the high-Z medium and dissipate all of their energy in a relatively short length. Improved manufacturing techniques had yielded a dense but transparent glass in which Cerenkov light could be efficiently coupled to good-quality photomultiplier tubes. The relatively small response of lead glass to pions and kaons compared to- electrons and photons is its'great advantage. Six months of hard work in Brookhaven test beams gave us a good command of and respect for this technique and its essential weakness, the calibration process.

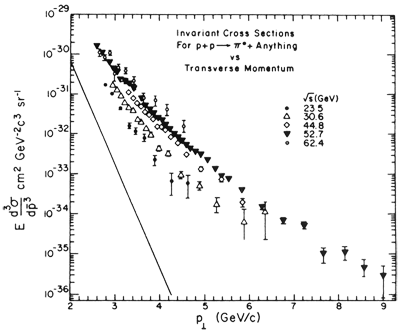
FIG. 9. Data from the yield of inclusive π0's.

The idea then was to have two arrays, on opposite sides of the .interaction point, each subtending about one steradian of solid angle. Figure 8 shows the CCR apparatus and Fig. 9 the data.

The CERN-Columbia-Rockefeller (CCR) team was assembled in 1971 to follow up on the BNL dilepton results, but now electron pairs were the particles of choice and a large lead-glass array was in place around the interaction point of this very first hadron collider. Here again, the discovery of the J/ψ was frustrated by an interesting background that was totally unexpected but, here again, a new technique for probing small distances was discovered -- the emission of high-transverse-momentum hadrons.

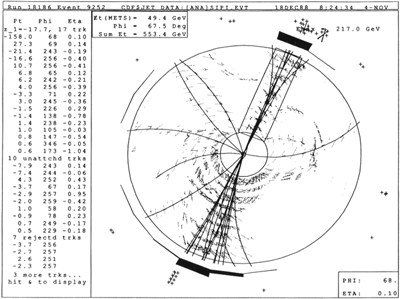
FIG. 10. CDF Fermilab dijet at 1.8 TeV.

Before the ISR research, a handy rule was that hadron production would fall exponentially with transverse momentum. The CCR result had, at a P_t of 3 GeV, orders of magnitude higher yield of single π⁰'s, well detected by the high-resolution lead-glass array. The production rate was observed to be

∼P_t^-8 at √s = 62 GeV,

which provided a stringent test of the quark-parton model in the early 1970s and QCD some few years later. Other ISR experiments quickly confirmed the CCR result, but only CCR had the quality and quantity of data to provide a phenomenological fit. It turned out that one could eventually go directly from these data to proton-parton (or quark-quark, etc.) hard scattering processes. The study of "single inclusive π⁰'s at high P_t" evolved into study of the more typical jet structure which now shows up so spectacularly in proton-antiproton collider data. See Fig. 10.

Thus the dilepton adventure using scintillation counters at BNL and the lead-glass exposures to the ISR initiated independent programs to contribute to the conviction that protons and pions are bound states of confined quarks interacting strongly via the exchange of gluons, which are themselves capable of becoming virtual qq pairs.

VI. The Third Generation: Observation of a Dimuon Resonance at 9.5 GeV in 400-GeV Proton-Nucleus Collisions (Herb et al., 1977)

In 1969-1970, the BNL dimuon result had stimulated not only the ISR proposal but also a proposal to Fermilab (then known as NAL and still a large hole in the ground) to do a high-resolution lepton pair experiment.

By the time the machine came on in 1972-1973, a single-arm lepton detector had been installed, using the very powerful combination of magnetic measurement and lead glass in order to identify electrons with a pion contamination of 10^-5. Such rejection is needed when only one particle is involved.

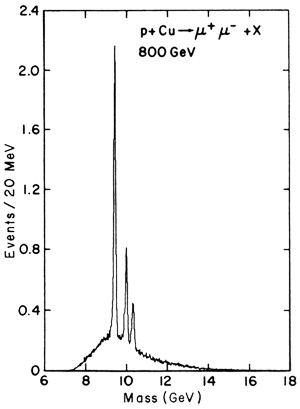
While the study of "direct" electrons fully occupied the ColumbiaFermilab-Stony Brook collaboration in 1974, the J/ψ was being cheerfully discovered at BNL and SLAC. The single-lepton effects turned out to be relatively unfruitful, and the originally proposed pair experiment got underway in 1975. In a series of runs the number of events with pair masses above 4 GeV gradually increased and eventually grew to a few hundred. During this phase, hints of resonant peaks appeared and then disappeared. The group was learning how to do those difficult experiments. In early 1977, the key to a vastly improved dilepton experiment was finally discovered. The senior Ph.D.'s on the collaboration, Steve Herb, Walter Innes, Charles Brown, and John Yoh, constituted a rare combination of experience, energy, and insight. A new rearrangement of target, shielding, and detector elements concentrated on muon pairs but with hadronic absorption being carried out in beryllium, actually 30 feet of beryllium. The decreased multiple scattering of the surviving muons reduced the mass resolution to 2%, a respectable improvement over the 10-15% of the 1968 BNL experiment. The filtering of all hadrons permitted over 1000 times as many protons to hit the target as compared to open geometry. The compromise between luminosity and resolution was optimized by meticulous attention to the removal of cracks and careful arrangement of the shielding. Recall that this kind of observation can call on as many protons as the detector can stand, typically 1% of the available protons. The multiwire proportional chambers and triggering scintillators were crowded in towards the target to get maximum acceptance. Muonness was certified before and after bending in iron toroids to redetermine the muon momentum and discourage punch-throughs. Figures 11(a) and 11(b) show the apparatus.

FIG. 11. (a) Plan view of the apparatus. Each spectrometer arm includes 11 PWC's P1-P11, 7 scintillating counter hodoscopes H1-H7, a drift chamber D1, and a gas filled threshold Cerenkov counter C.	FIG 11. (b) Schematic sketch of Fermilab diinuon experiment that led to the discovery of the upsilon particle.

In a month of data taking in the spring of 1977, some 7000 pairs were recorded with masses greater than 4 GeV and a curious, asymmetric, and wide bump appeared to interrupt the Drell-Yan continuum near 9.5 GeV. With 800 events in the bump, a very clean Drell-Yan continuum under it, and practically no background as measured by looking (simultaneously) for same-sign muons, the resonance was absolutely clear. It was named upsilon and a paper was sent off in August of 1977. By September, with 30,000 events, the enhancement was resolved into three clearly separated peaks, the third "peak" being a well-defined shoulder. See Figs. 12(a) and 12(b). These states were called Υ, Υ', and Υ". Shortly afterwards, the DORIS accelerator in DESY produced the upsilon in e⁺e^- collisions and also served to confirm the only plausible interpretation of the upsilon as a bound state of a new quark b with its antiparticle b. The Υ' and Υ" were then the 2S and 3S states of this nonrelativistic "atom." In the Standard Model, we had a choice of chargte, +2/3 (uplike) or -1/3 (downlike) for the b quark. The Fermilab data favored -1/3.

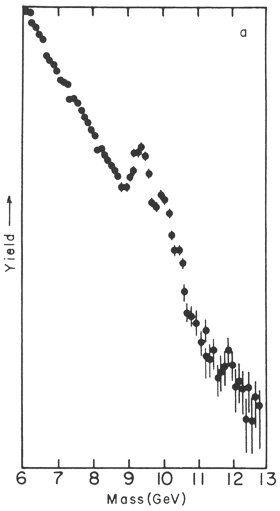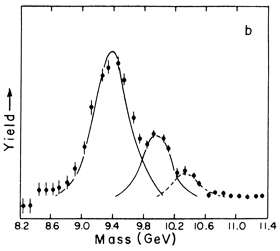FIG. 12. (a) - Peaks on Drell-Yan continuum. (b) Peaks with continuum subtracted.

Fallout was relatively swift. Taken together with the discovery by Martin Perl (1987) and his colleagues of the τ lepton at SLAC slightly earlier, a third generation was added to the Standard Model with the b quark at 5 GeV and the τ lepton at 2 GeV. This fully confirmed the KM speculation that CP violation may require a third generation. (Clearly we are vastly oversimplifying the theoretical efforts here.)

FIG. 13. Fermilab E-605 data.

The bb system was a beautiful addition to cc (charmonium) as a measurement laboratory for the study of potential models for the strong quark-quark force. To get in on the fun, I organized a group from Columbia and Stony Brook to design a lead-glass, sodium iodide spectrometer to be used at the CESR machine, ideally suitable for Y spectroscopy. This Columbia, Stony Brook collaboration (CUSB) began taking data in 1979 and soon assisted in the identification of the 4S state (Finocchiaro et al., 1980). The 4S state is especially important because it is above threshold for hadronic decay to B states, i.e., mesons having one b quark and a lighter antiquark. Followup experiments to learn more about the upsilons were also carried out at Fermilab. These used a number of tricks to advance even further the resolving power without losing luminosity — see Fig. 13. By now many other states, including p states, have been identified in this new heavy-quark spectroscopy.

Recent studies of the B states in electron-positron colliders indicate that the B system may be far richer in physics than the charm equivalent, the D system. B⁰'s mix like the K⁰ and K⁰ particles. Quoting one of CERN's leading phenomenologists, G. Altarelli: "The observation by Argus at DESY of a relatively large amount of B⁰—B0 mixing ... was the most important experimental result of the year [1987] in particle physics." There is the strong possibility that CP violation, seen to date only in the K⁰ system, may possibly be observable in the B⁰ system. B factories, usually high-intensity e⁺e^- machines, are being proposed in various labs around the world. The Cornell machine is being upgraded to produce of the order of 10⁶ BB pairs a year. Meanwhile the hadron machines are trying hard to solve the very difficult experimental problem of detecting B's (e.g., at the 800-GeV Fermilab fixed target) in a background of 10⁶ times as many inelastic collisions. An ambitious detector is being proposed for the Fermilab collider, with the goal of obtaining 10¹⁰ BB pairs/year. Judging from 1988 activity, measurements in B physics will play an increasingly important role in particle research over the next decade. The driving force is the recognition that the third generation seems to be needed to account for CP violation. Taken together with baryon nonconservation, CP violation plays a key role in our understanding of the evolution of the universe, including why we are here. For physicists with a less grandiose view, the quark mixing matrix parameters are part of the basis of our Standard Model, and b physics is the key to these crucial parameters.

The third generation still needs a top quark and, as we speak here, searches for this are going on now at the CERN SppS machine and at the Fermilab collider.

Both machines are operating at very good intensities averaging 200-400 nb^-1 per week. The Fermilab machine has a decided advantage of 1.8 TeV as compared to CERN's 0.63 TeV but everything depends on the quality of data, the wisdom invested in the design of the detectors, and, of course, the mass of the quark. It does seem safe to predict that a paper will soon appear, perhaps entitled "Observation of the Top Quark."

VII. Crucial Issues in Neutrino Physics Today

I conclude this paper with a brief résumé of our ignorance about neutrinos. Neutrino interaction data are in good agreement with electroweak theory of the Standard Model and so they will continue to be used to improve our knowledge of quark structure functions, the crucial Weinberg angle, etc. However, we have not yet seen the ν_τ, we do not know if there is a fourth neutrino, we cannot answer urgent questions about the possibility of neutrino mass, and mixing of different flavors, of the stability of the neutrino, whether it has a magnetic moment, and, finally, the nature of the antineutrino, e.g., whether of the Dirac or Majorana type. What makes all of this intensely interesting are two factors: (1) the awesome astrophysical implications of the answers to these questions and (2) the view as expressed by Weinberg that ". . . neutrino mass illuminates some of the deepest questions in particle physics." This is because, in the Standard Model, with the usual quarks, leptons, and gauge bosons, there is no possible renormalizable interaction that can violate lepton number conservation and give the neutrino a mass. Thus the observation of mass would very likely be a sign of new physics far beyond the Standard Model, perhaps as far as 10¹⁵ GeV, the scale of Grand Unification.

A. The third neutrino, ν_τ

The "three-neutrino" experiment has not been done. Although data from the decay of the r lepton are very strongly suggestive of the existence of ν_τ, direct evidence for ν_τ has yet to appear.

The technical problem is to move the target as close to the detector as possible but to divert the now unstoppable muons by magnetic sweeping. The flux of ν_τ's cannot be predicted with confidence, and the shielding configuration is very expensive. This is primarily why the experiment has not yet been done.

B. A fourth neutrino?

This question is a shorthand for the issue of the number of generations. Searches for heavier quarks and/or leptons are the sine qua non of new accelerators, and these have all been negative so far, although the results simply give limits M_Q > 40 GeV (same as the top quark) and M_L > 20-40 GeV depending upon the kind of heavy lepton and upon assumptions as to the mass of its accompanying neutrino (Perl, 1987). Important constraints come from astrophysics, where the abundance of helium has been related to the number of low-mass neutrinos (Steigman et al., 1977). Probably one more low-mass neutrino could still be accommodated within the Big Bang nucleosynthesis arguments. The connection between the cosmological model of creation in the Big Bang and the number of generations in the Standard Model is one of the more romantic episodes in the marriage of particle physics and (early universe) cosmology. In fact, one of the strongest supports of Big Bang cosmology is primordial nucleosynthesis: the cooking of the light elements in the caldron beginning at t 1 sec. The astrophysicists manage to get it right: the abundances of deuterium, helium, and lithium. The key is helium 4; its abundance is a sensitive indicator of the total radiation density at formation time. Contributing to this are all the low-mass, relativistic particles, i.e., photons, electrons, and the three neutrinos plus their antiparticles. Another generation containing a lowmass neutrino would probably not destroy the agreement, but it would begin to stretch the agreement. Conclusion: there may be a fourth generation, but a fifth generation which included low-mass particles would provide a major problem for our astrophysical colleagues. Of course there could be something out there which is outside of the generational structure. One experiment soon to yield results is being carried out at the e⁺e^- machines at CERN's Large Electron Positron Collider (LEP) and the Stanford Linear Collider (SLC) where the width of the Z⁰ will give some indication of the number of neutrino pairs into which it can decay. The residual and dominant current interest in the neutrinos comes from astrophysical arguments related to dark matter. This in turn puts the spotlight on the neutrino mass measurements to which we now turn.

C. Neutrino masses and oscillation

In the Standard Model (SM), neutrino masses are set to zero and both total lepton number L and lepton flavor number L_i (i=e,μ,τ) are conserved. Neutrino masses "provide a window on the world beyond the SM" and have become one of the outstanding concerns of present-day particle physics. The possibility of oscillation is a statement that ν_μ→ν_e is not rigorously forbidden as suggested by our two-neutrino experiment. The issue is given great emphasis by the cosmologists, who are increasingly impinging on the orderly developments of particle physics (and what a joy that is) and by the solar neutrino crisis, which has been around for decades. This is the discrepancy between the number of ν_e's observed to be coming from the Sun and the flux that our best knowledge would predict. The detection of v signals from supernova 1987A has added to the intensity of interest.

The oscillation possibility was first suggested by B. Pontecorvo in 1967 (Pontecorvo, 1967). The neutrino flavor mixing is analogous to the quark mixing as given in the KM matrix. Today we see many attempts to observe . oscillations. These are at the high-energy accelerator labs, at meson factories, at reactors, and indeed in the solar environment. There, the problem is a theoretical one, to understand the lack of neutrinos from the processes that are known to keep the Sun shining. The solar neutrino crisis alone is receiving the attention of at least 14 large experimental groups around the world and many times that number of theorists.

As of this date, no convincing evidence for oscillations or for neutrino masses has been observed. These indirect evidences for mass differences and other experiments which look directly for neutrino masses are summarized as follows:

m(ν_e) 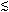20 eV,

m(ν_μ) < 0.25 MeV,

m(ν_τ) < 35 MeV.

Oscillation limits are more conventionally given in terms of limits on the mass differences Δ and the coupled limits on the phase angle θ that defines the mixing strength. Slowly and inexorably the space on the two-dimensional plot (Δ² vs sin2θ) is being reduced to the lower left-hand corner, although logarithmic scales will encourage experimenters to design ever more sensitive tests.

Cosmologists assure us that we live in a universe whose primary component of mass density is dark (nonluminous) and is presently unidentified. Much of this is probably (they say) nonbaryonic, and some kind of weakly interacting particle carrying some mass (WIMP) is a likely candidate. The principle of minimum complexity would have these be neutrinos, and the condition is Σm_i ~20 eV (i =e,μ,τ). This brings the ν_τ forward, as emphasized by Harari, who proposes as a matter of urgency a renewed search for ν_μ->ν_τ,.

Other experiments occupying the new pion factories (SIN, TRIUMF, and LAMPF) look for (small) violations of lepton flavor conservation via extremely sensitive searches for such reactions as μ⁺/→e⁺+γ (again, but now at B~10^-11) and μ⁺/→e⁺e⁺e^- (B<10^-12). The improvements in experimental techniques and machines conspire to improve these observations by about an order of magnitude every seven years. For completeness we must also list the search for rare decay modes of K mesons in "kaon factories." Pion, kaon, and B factories clearly indicate the industrialization of particle physics. The physics objectives of all of these researches are to seek out the tiny influences of presumed new physics which is taking place at the TeV level and higher. For a mature experimenter, these are fun experiments combining the payoff of observations (if and when) with the attention to detail of precise measurements.

To all of the above we should add the new generation structure function research with neutrino beams, probably tagged. The 1962 twoneutrino experiment honored at this meeting has given rise to a set of activities that, taken together in 1988, continue to play a dominating role in particle physics and its new branches, astrophysics and early universe cosmology.

VIII. Final Comments

I would like to conclude this history of the Standard Model which is not a history at all. From time to time it follows the main road, e.g., when the two-neutrino experiment pointed to flavor and the generational organization of the Standard Model. More often it takes side trails because my own experiments were down those paths. So we have neglected such milestones as the discovery of neutral currents, the τ lepton, the W and Z bosons, charmonium, etc. We have also been crushingly4 neglectful of the essential theoretical contributions and blitzed through quarks, color, symmetry-breaking, etc.

However, I regret most not having the space to speak more of the accelerators, the detectors, and the people who brought these to be. The Nevis cyclotron was built under the leadership of Eugene Booth and James Rainwater; the AGS, most successful machine ever, led by Ken Green, Ernest Courant, Stanley Livingston, and Hartland Snyder; Fermilab, of course, by Robert Wilson and his outstanding staff. My own detector experience owes much to Georges Charpak of CERN and William Sippach of Columbia. In neglecting these details I am reminded of my teacher, friend, and thesis professor, Gilberto Bernardini, who, when being shown the Nevis cyclotron's innards, exclaimed: "Just show me where the beam comes out." Finally, I make amends to the theorists, who are obviously crucial to the entire enterprise. I have enjoyed and profited from many physicists of the theoretical persuasion but most especially T. D. Lee, M. Veltman, and J. D. Bjorken.

References

Aubert, J. J., U. Becker, P. J. Biggs, J. Burger, M. Chen, G. Everhart, P. Goldhagen, J. Leong, T. McCorriston, T. G. Rhoades, M. Rohde, Samuel C. C. Ting, and Sau Lan Wu, 1974, Phys. Rev. Lett. 33,1404.

Bardon, M., et al., 1958, Phys. Rev. 110, 780.

Berman, S. M., J. D. Bjorken, and J. B. Kogut, 1971, Phys. Rev. D 4, 3388.

Bjorken, J. D., and S. L. Glashow, 1964, Phys. Lett. 11, 255.

Blumenfeld, H., W. Chinowsky, and L. M. Lederman, 1958, Nuovo Cimento 8, 296.

Burns, R., G. Danby, E. Hyman, L. M. Lederman, W. Lee, J. Rettberg, and J. Sunderland, 1965, Phys. Rev. Lett. 15, 830.

Büsser, F. W., L. Camilleri, L. DiLella, G. Gladding, A. Placci, B. G. Pope, A. M. Smith, J. K. Yoh, E. Zavattini, B. J. Blumenfeld, L. M. Lederman, R. L. Cool, L. Litt, and S. L. Segler, 1973, Phys. Lett. B 46, 471.

Byfield, H., J. Kessler, and L. M. Lederman, 1952, Phys. Rev. 86, 17.

Christenson, J. H., J. W. Cronin, V. L. Fitch, and R. Turlay, 1964, Phys. Rev. Lett. 13, 138.

Christenson, J. H., G. S. Hicks, L. M. Lederman, P. J. Limon, B. G. Pope, and E. Zavattini, 1970, Phys. Rev. Lett. 25, 1523.

Coffin, T., R. L. Garwin, L. M. Lederman, S. Penman, and A. M. Sachs, 1957, Phys. Rev. 106, 1108.

Danby, G., J-M. Gaillard, K. Gouliancis, L. M. Lederman, N. Mistry, M. Schwartz, and J. Steinberger, 1962, Phys. Rev. Lett. 9, 36.

Devons, S., G. Gidal, L. M. Lederman, and G. Shapiro, 1960, Phys. Rev. Lett. 5, 330.

Ellsworth, R. W., A. C. Melissinos, J. H. Tinlot, H. von Briesen, Jr., T. Yamanouchi, L. M. Lederman, T. Tannenbaum, R. L. Cool, and A. Maschke, 1968, Phys. Rev. 165, 1449.

Feinberg, G., 1958, Phys. Rev. 110, 1482.

Finocchiaro, G., G. Giannini, J. Lee-Franzini, R. D. Schamberger, Jr., M. Siverta, L. J. Spencer, P. M. Tuts, T. Bohringer, F. Costantini, J. Dobbins, P. Franzini, K. Han, S. W. Herb, D. M. Kaplan, L. M. Lederman, G. Mageras, D. Peterson, E. Rice, J. K. Yoh, and G. Levman, 1980, Phys. Rev. Lett. 45, 222.

Garwin, R. L., L. M. Lederman, and M. Weinrich, 1957, Phys. Rev. 105, 1415.

Gell-Mann, M., and A. Pais, 1955, Phys. Rev. 97,1387.

Glashow, S. L., J. Iliopolis, and L. Maiani, 1970, Phys. Rev. D 2, 1285.

Herb, S. W., D. C. Hom, L. M. Lederman, J. C. Sens, H. D Snyder, J. K. Yoh, J. A. Appel, B. C. Brown, C. N. Brown, W. R. Innes, K. Ueno, T. Yamanouchi, A. S. Ito, H. Jostlein, D. M. Kaplan, and R. D. Kephart, 1977, Phys. Rev. Lett. 39, 252.

Ito, A. S., R. J. Fisk, H. Jostlein, D. M. Kaplan, S. W. Herb, D. C. Hom, L. M. Lederman, H. D. Snyder, J. K. Yoh, B. C. Brown, C. N. Brown, W. R. Innes, R. D. Kephart, K. Ueno and T. Yamanouchi, 1981, Phys. Rev. D 23, 604.

Kaplan, D. M., R. J. Fisk, A. S. Ho, H. Jostlein, J. A. Appel, B. C. Brown, C. N. Brown, W. R. Innes, R. D. Kephart, K. Ueno, T. Yamanouchi, S. W. Herb, D. C. Hom, L. M. Lederman, J. C. Sens, H. D. Snyder, and J. K. Yoh, 1978, Phys. Rev Lett. 40, 435.

Lande, K., E. T. Booth, J. Impeduglia, and L. M. Lederman, 1956, Phys. Rev. 103, 1901.

Lederman, L. M., 1951, Ph.D. thesis (Columbia University).

Lederman, L. M., E. T. Booth, H. Byfield, and J. Kessler, 1951, Phys. Rev. 83, 685.

Lederman, L. M., J. Tinlot, and E. Booth, 1951, Phys. Rev. 81, 281.

Lee, T. D., Reinhard Oehme, and C. N. Yang, 1957, Phys. Rev. 106, 340.

Lee, T. D., and C. N. Yang, 1956, Phys. Rev. 104, 254.

Meyer, S. L., E. W. Anderson, E. Bleser, L. M. Lederman, J. L. Rosen, J. Rothberg, and IT. Wang, 1963, Phys. Rev. 132, 2693.

Okun, L., 1966 (unpublished).

Perl, Martin, 1987, in Proceedings of the XXIII International Conference on High Energy Physics, Berkeley, 1986, edited by S. C. Loken (World Scientific, Singapore), Vol. I, p. 596.

Pontecorvo, B., 1967, Zh. Eksp. Teor. Fiz. 53, 1717 [Sov. Phys. JETP 26, 984 (1968)].

Sargent, C. P., M. Rinehart, L. M. Lederman, and K. C. Rogers, 1955, Phys. Rev. 99, 885.

Steigman, Gary, David N. Schramm, and James E. Gunn, 1977, Phys. Lett. B 66, 202.

Yamaguchi, Y., 1966, Nuovo Cimento A 43,193.

---

Thanks

This publication was selected from the treasures of the Fermilab Archives.

Back to Top